
 |
ESTADÍSTICA ELEMENTAL |
Diferentes estudios, diferentes resultados
Marc Saez y Maria Antònia Barceló
Profesores de Estadística y Econometría
Grupo de Investigación en Estadística, Economía Aplicada y Salud (GRECS)
Universidad de Girona
Las investigaciones desarrolladas durante las últimas décadas han demostrado que las personas obesas tienen más riesgo de sufrir infartos, diabetes y otras enfermedades que las personas con peso normal. Para saber si una persona es obesa se calcula el Índice de Masa Corporal, dividiendo su peso en kilogramos entre el cuadrado de su altura en metros.
Si pretendiésemos estudiar el porcentaje de personas obesas en una Comunidad Autónoma de España, no podríamos medir el peso y la altura de toda la población, puesto que se necesitarían muchos recursos y tiempo para realizar el estudio.Se debe recurrir a una muestra de ciudadanos y ciudadanas elegida al azar que sea representativa de esa población. El porcentaje de personas obesas que hay en la muestra se considerará una aproximación del porcentaje de personas obesas que hay en la población. El objetivo de trabajar con una muestra representativa es, por tanto, obtener resultados que luego puedan ser trasladados al conjunto de la población. Es lo que se conoce técnicamente como inferencia.
Según la Encuesta Nacional de Salud de 2006, el 15% de la población adulta de Cataluña era obesa. Sin embargo, el mismo año, la Encuesta Catalana de Salud estimaba que el porcentaje de adultos obesos era de 13%. ¿Por qué los resultados de ambos estudios fueron diferentes?
Mostraremos un pequeño ejemplo para aclararlo. Supongamos que la población está compuesta por sólo 5 personas. Cada una de ellas está representada por un cuadrado de color celeste si su peso es normal y rojo si es obesa. La letra situada en el centro del cuadrado es la inicial del nombre de la persona.
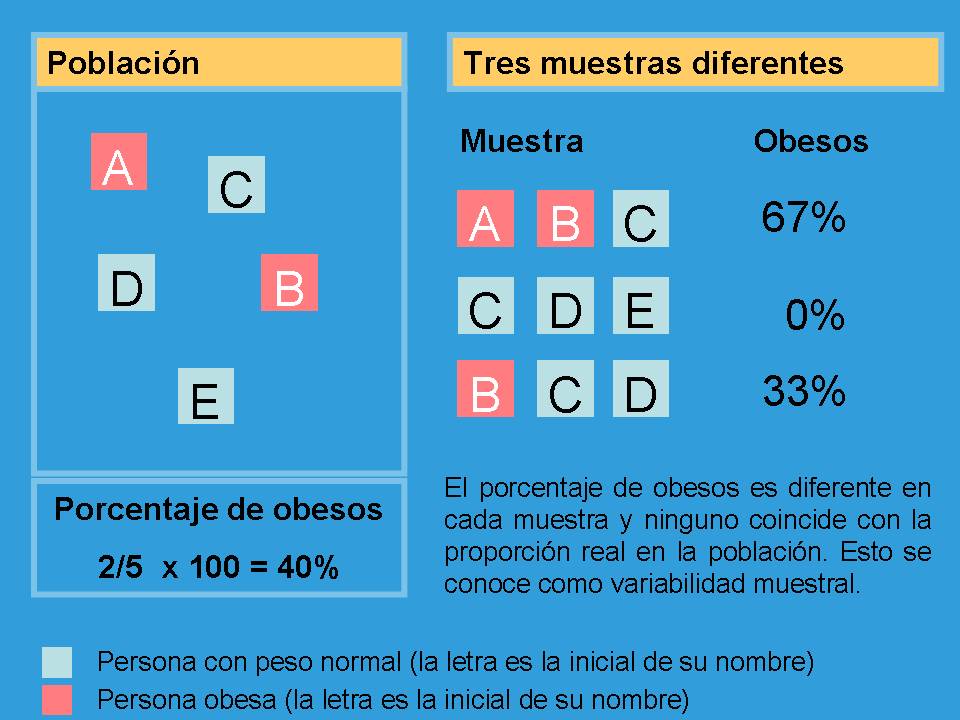
En este caso, 2 de las 5 personas que componen la población son obesas, es decir, el porcentaje de personas obesas real es del 40% (2/5 x 100). Sin embargo, cuando no es posible observar a todos los miembros de una población es necesario seleccionar una muestra aleatoria y estimar en ella la proporción de personas obesas. Si se escogen 3 personas aleatoriamente, el azar podría llevar a estudiar a cualquiera de los grupos que aparecen en la parte derecha de la figura anterior.
En la primera muestra, el porcentaje de personas obesas es 67%, mientras que en la última 33%. Todos los porcentajes son diferentes y ninguno coincide exactamente con la proporción de personas obesas real de la población. Sin embargo, todos los resultados son igualmente válidos como aproximaciones a la proporción de obesos de la población, por cuanto se han calculado utilizando muestras aleatorias de la misma.
Los resultados obtenidos con una muestra de personas siempre serán diferentes a los que se podrían haber obtenido con otra muestra. Por este motivo, no es posible conocer exactamente el porcentaje real de obesos en la población utilizando los datos de una muestra, aunque sí es posible determinar un rango de valores que, con una probabilidad alta, contiene el verdadero porcentaje de obesos de la población. De esta forma, con los datos de la primera muestra de personas no se podrá afirmar que el porcentaje de obesos en la población sea exactamente 67%. Sin embargo, existen procedimientos matemáticos mediante los que es posible predecir, usando la información de esa misma muestra, que el porcentaje de obesos en la población se encuentra entre 21% y 94% con casi total seguridad. Es lo que se denomina intervalo de confianza, y en este caso la predicción que realiza es correcta.
Cuando se trabaja con muestras, diferentes investigaciones ofrecerán diferentes resultados. Esta variabilidad podría explicar por qué dos estudios de opinión obtienen conclusiones diferentes cuando hacen sondeos de intención de voto. Ofrecer un intervalo de confianza junto a las estimaciones aportaría una información adicional muy valiosa para conocer el error cometido en las predicciones.
Julio de 2011











